Opening Remarks
- This is going to be a long post, and as always, it will take time to gradually be completed.
- I would appreciate it if you could correct me if I’m wrong on any part of this post.
- In each section, we’ll first explore the intuitive concepts to build a basic understanding. Then, we’ll go through the formal mathematical framework, and finally, we’ll implement it in PyTorch.
- This post is a simple review of my understanding of diffusion models. At first glance, it may not seem directly related to diffusion models because I’ll also be discussing classic generative models like score-based models and energy-based models alongside diffusion models. For now, think of it as nothing more than my personal notes.
- I strongly recommend reading the papers listed in the resources alongside this post. Many of the explanations here are simply expansions of the concepts discussed in those papers.
introduction
We can imagine our perceptions as low-dimensional shadows of a higher-dimensional space. The best way to think about it is Plato’s allegory of the cave: some people are tied in a cave, and everything they can see is 2D shadows of 3D objects outside the cave. Likewise, we can think of our observations as lower-dimensional shadows of higher-dimensional objects. But there is a difference between this analogy and what we are seeking for in generative modeling. In generative modeling, instead of trying to model higher-dimensional representations of our observations, we look for lower-dimensional representations of them. Mathematically, we can write the joint probability distribution of these lower-dimensional distributions and our observations as :
\[p(x) = \int p(x,z) \, dz \quad(1)\]In this equation, we are calculating p(x) by marginalizing out z, we can also write:
\[p(x) = \frac{p(x,z)}{p(z|x)} \quad(2)\]This is comes from applying Bayes’ theorom.
However, calculating p(x) using these two equations is not practical because it either requires integrating over the latent space z, which is too hard, or having access to ground truth z, which is not tractable in complex models in practice. Consequently, instead of maximizing p(x), we should seek a proxy to optimize. Here is where the ELBO (Evidence Lower Bound) comes into play. Instead of directly maximizing \(\log p(x)\), we seek for other feasibly tractabile function to maximize. If we find a function that is equal or lower than our original object \(\log p(x)\) everywhere, we can be sure that maximizing this proxy function will indirectly lead to maximizing our original funtion \(\log p(x)\). to better understand this, see image below.
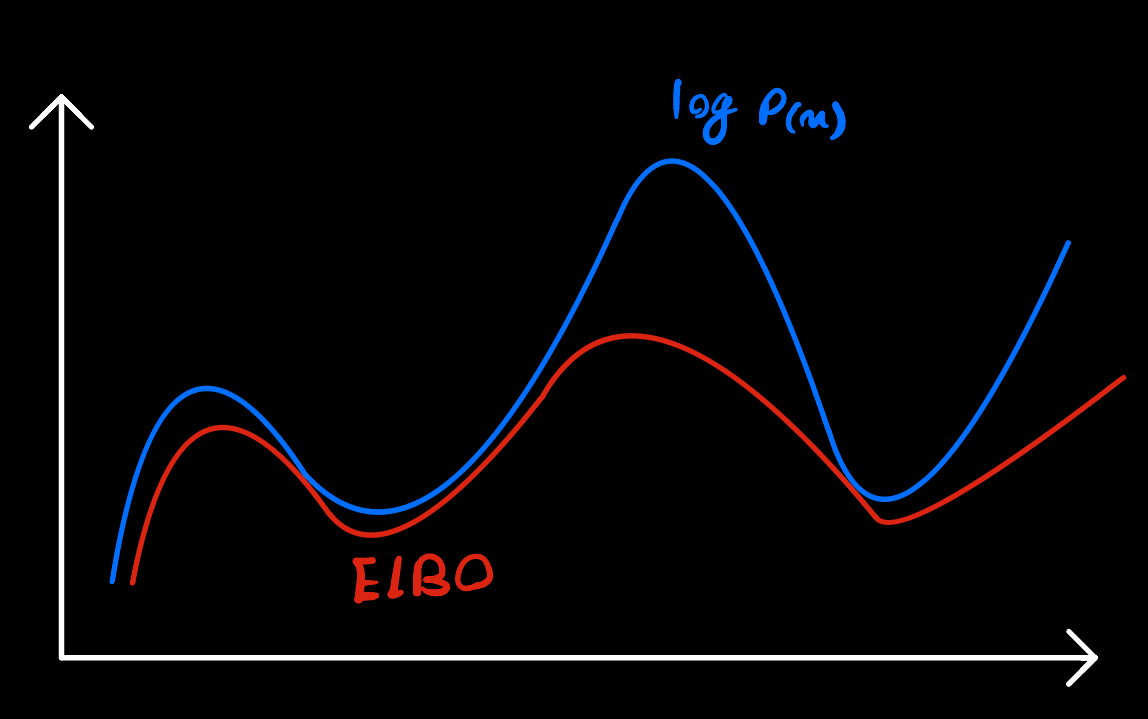
We can mathematically prove following. The right expression is what we call ELBO.
\[\log p(x) \geq \mathbb{E}_{q_\phi(z|x)} \left[ \log \frac{p(x,z)}{q_\phi(z|x)} \right] \quad(3)\]$q_\phi$ is a prediction of latent variable $z$ with parameters $\phi$
\[\begin{aligned} \log p(x) &= \log \int p(x, z) \, dz &\text{Equation 1} \quad (4) \\ &= \log \int \frac{p(x, z) \cdot q_\phi(z|x)}{q_\phi(z|x)} \, dz & \text{Multiply by one} \quad (5) \\ &= \mathbb{E}_{q_\phi(z|x)} \left[ \log \frac{p(x,z)}{q_\phi(z|x)} \right] & \text{Definition of Expectation} \quad (6) \\ &\geq \mathbb{E}_{q_\phi(z|x)} \log \left[\frac{p(x,z)}{q_\phi(z|x)} \right] & \text{Jensen's Inequality} \quad (7) \end{aligned}\]But we don’t have intuition on why Jensen’s Inequality leads us to this result, so let’s write it in another way:
\[\begin{aligned} \log p(x) &= \log p(x) \int q_\phi(z|x) \, dz \quad &\text{(Multiply by } 1 = \int q_\phi(z|x) \, dz) \quad(8)\\ &= \int q_\phi(z|x) \, (\log p(x)) \, dz \quad &\text{(Bring evidence into integral)} \quad(9)\\ &= \mathbb{E}_{q_\phi(z|x)} \left[ \log p(x) \right] \quad &\text{(Definition of Expectation)} \quad(10)\\ &= \mathbb{E}_{q_\phi(z|x)} \left[ \log \left(\frac{p(x, z)}{p(z|x)} \right) \right] \quad \quad(11)\\ &= \mathbb{E}_{q_\phi(z|x)} \left[ \log \left(\frac{p(x, z) \cdot q_\phi(z|x)}{p(z|x) \cdot q_\phi(z|x)} \right) \right] \quad &\text{(Multiply by } 1 = \frac{q_\phi(z|x)}{q_\phi(z|x)}) \quad(12) \\ &= \mathbb{E}_{q_\phi(z|x)} \left[ \log \left(\frac{p(x, z)}{q_\phi(z|x)} \right) \right] + \mathbb{E}_{q_\phi(z|x)} \left[ \log \left(\frac{q_\phi(z|x)}{p(z|x)} \right) \right] \quad &\text{(Split the Expectation)} \quad(13) \\ &= \mathbb{E}_{q_\phi(z|x)} \left[ \log \left(\frac{p(x, z)}{q_\phi(z|x)} \right) \right] + D_{\text{KL}} \left( q_\phi(z|x) \parallel p(z|x) \right) \quad &\text{(Definition of KL Divergence)} \quad(14)\\ &\geq \mathbb{E}_{q_\phi(z|x)} \left[ \log \left(\frac{p(x, z)}{q_\phi(z|x)} \right) \right] \quad &\text{(KL Divergence always } \geq 0) \quad(15) \end{aligned}\]Evidence (\(\log p(x)\)) is equal to ELBO plus a KL divergence term, which is always non-negative. Accordingly, ELBO never exceeds the evidence term. The KL divergence term measures the difference between the true posterior distribution $p(z \mid x)$ and the model’s approximation of it, $q_\phi(z \mid x)$, which is also called the approximate posterior. By reducing this KL term, we make these two distributions closer. Ideally, we want them to exactly match, making the KL term zero. We know that $(x)$ doesn’t depend on $\phi$, therefore it is a constant with respect to $\phi$. We can notice that the ELBO term and the KL term sum up to a constant number. We use this fact to indirectly minimize the KL term by maximizing the ELBO term. We can’t calculate the KL term directly because we don’t have ground truth posterior $p(z \mid x)$. By maximizing the ELBO, we aim to improve the model’s approximation of the true posterior distribution, since a higher ELBO implies a lower KL divergence, bringing the approximate and true posterior distributions closer together.
Before diving deep into diffusion models, lets first take a look to vaariational autoencoder models (VAEs). VAEs consist of two parts: a encoder $q_\phi (z \mid x)$ which transforms the input into a distribution over the possible latents, and a decoder $p_\phi (x \mid z)$ that converts a given latent z into an observation x. Lets write ELBO term with some modificatons.
\[\begin{aligned} \mathbb{E}_{q_\phi(z|x)} \left[\log \frac{p(x,z)}{q_\phi(z|x)}\right] &= \mathbb{E}_{q_\phi(z|x)} \left[\log \frac{p_\theta(x|z)p(z)}{q_\phi(z|x)}\right] \quad \text{(Chain Rule of Probability)} \quad(16)\\ &= \mathbb{E}_{q_\phi(z|x)} [\log p_\theta(x|z)] + \mathbb{E}_{q_\phi(z|x)} \left[\log \frac{p(z)}{q_\phi(z|x)}\right] \quad \text{(Split the Expectation)} \quad(17)\\ &= \underbrace{\mathbb{E}_{q_\phi(z|x)} [\log p_\theta(x|z)]}_{\text{reconstruction term}} - \underbrace{D_\text{KL}(q_\phi(z|x) \| p(z))}_{\text{prior matching term}} \quad \text{(Definition of KL Divergence)} \quad(18) \end{aligned}\]As you can see it consists of two parts, a recostruction part and a prior matching part. The reconstruction term ensures that decoser can reconstruct the input data given the latent representation z. The prior matching term encourages learned distribution $q_\phi (z \mid x)$ to be close to the prior $p(z)$. Finally maximizing ELBO is equivalent to maximizing the first term and minimizing the second term.